Cards

# adapted from https://github.com/kach/memo/blob/main/demo/Memonomicon.ipynb
import jax
import jax.numpy as np
from memo import memo

cards = np.array([1, 2, 3])

@memo(save_comic="memo-comic-card")
def alice_chooses_card_E():
    alice: chooses(c in cards, wpp=1)
    return E[alice.c]

# Comic representation of the modeling: ./memo-comic-card.png

print(alice_chooses_card_E())

2.0

Basic conditioning

from memo import memo
import jax.numpy as np

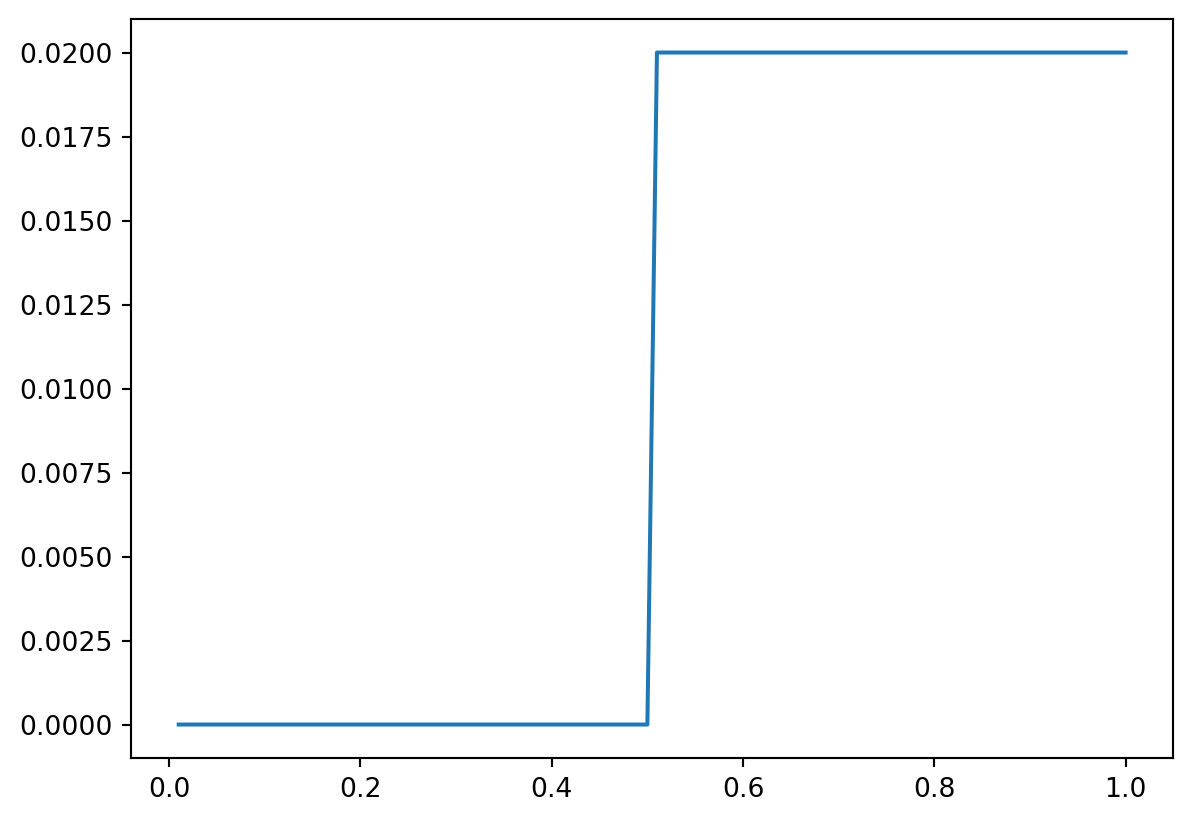
possible_values = np.array(range(1,101)) / 100

@memo(save_comic="memo-comic-bc")
def model[query_v: possible_values]():
    # establish prior in the observer's frame: that a value generator has some value from .01 to 1
    value_gen: given(v in possible_values, wpp=1)
    
    # push an observation into a valuator's frame:
    # first, establish the prior in the valuator's frame: have the valuator model that the value generator chose a value uniformly at random
    valuator: thinks[ value_gen: given(v in possible_values, wpp=1) ]
    # then, now that the value is modeled by the valuator, condition that value
    valuator: observes_that [value_gen.v > .5]

    # return the estimated probability of the generator's value for being each queried v, *estimated according to the valuator/from the valuator's frame*
    valuator: knows(query_v) # first, push query_v into the frame of the valuator
    return valuator[Pr[value_gen.v == query_v]]

    # or return the expected value in the valuator's frame:
    # return valuator[E[value_gen.v]]

# Comic representation of the modeling: ./memo-comic-bc.png

from matplotlib import pyplot as plt
plt.plot(possible_values, model())